THEORY OF TENSILE STRENGTH AND TENSILE STRESS.

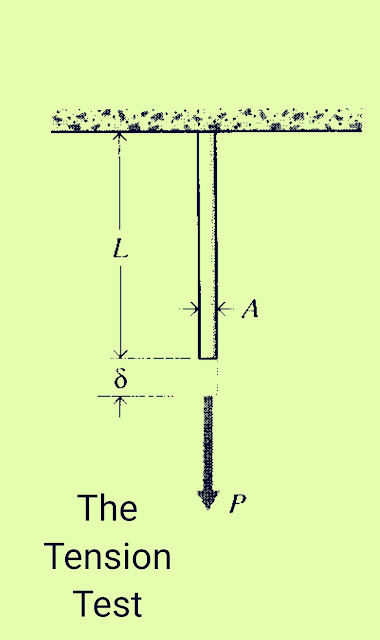
TENSILE STRENGTH AND TENSILE STRESS  

Perhaps the most natural test of material’s mechanical properties is the tension test, in which a strip or cylinder of the material, having length 'L' and cross-sectional area A, is anchored at one end and subjected to an axial load P – a load acting along the specimen’s long axis – at the other. As the load is increased gradually, the axial deflection 'δ' of the loaded end will increase also. Eventually the test specimen breaks or does something else catastrophic, often fracturing suddenly into two or more pieces. (Materials can fail mechanically in many different ways for instance, recall how blackboard chalk, a piece of fresh wood, and Silly Putty break.) As engineers, we naturally want to understand such matters as how 'δ' is related to 'P', and what ultimate fracture load we might expect in a specimen of different size than the original one. As materials technologists, we wish to understand how these relationships are influenced by the constitution and microstructure of the material.

One of the pivotal historical developments in our understanding of material mechanical proper-ties was the realization that the strength of a uniaxially loaded specimen is related to the magnitude of its cross-sectional area. This notion is reasonable when one considers the strength to arise from the number of chemical bonds connecting one cross section with the one adjacent to it as depicted in, where each bond is visualized as a spring with a certain stiffness and strength. Obviously, the number of such bonds will increase proportionally with the section’s area1. The axial strength of a piece of blackboard chalk will therefore increase as the square of its diameter. In contrast, increasing the length of the chalk will not make it stronger (in fact it will likely become weaker, since the longer specimen will be statistically more likely to contain a strength-reducing flaw).

When reporting the strength of materials loaded in tension, it is customary to account for the effect of area by dividing the breaking load by the cross-sectional area:

                        [ σf = Pf/A0 ]

where 'σf' is the ultimate tensile stress, often abbreviated as UTS, 'Pf' is the load at fracture, and 'A0' is the original cross-sectional area. (Some materials exhibit substantial reductions in cross-sectional  area as they are stretched, and using the original rather than final area gives the so-call engineering strength.) The units of stress are obviously load per unit area, N/m^2 (also called Pascals, or Pa) in the SI system and lb/in^2 (or psi) in units still used commonly in the United States.

If the specimen is loaded by an axial force 'P' less than the breaking load 'Pf' , the tensile stress is defined by analogy  with equation.

                       [ σ = P/A0 ]

The tensile stress, the force per unit area acting on a plane transverse to the applied load, is a fundamental measure of the internal forces within the material. Much of Mechanics of Materials is concerned with elaborating this concept to include higher orders of dimensionality, working out methods of determining the stress for various geometries and loading conditions, and predicting what the material’s response to the stress will be.

* Equation figure- 

The Theory of Tensile Strength and Tensile Stress.

#fiza engineer............@ sk najmul  ( munna )

Share :

Facebook Google+ Twitter

Related Posts :